Final Project: Transformer Knowledge Distillation

After learning about the Transformer and it’s incredible capacity to work with language, I was I excited to integrate it into a tool for people to use. I had thought about using it for question answering, text summarization, or natural language generation, so I decided to play with BERT on my laptop. My computer was huffing and puffing, and running out of RAM. Given all this trouble a laptop was having, I couldn’t have imagine what would happen if I tried to run BERT on a phone. This gave me inspiration to consider training smaller transformer language models with similar levels of performance to the big models.

• Introduction: Transformer Success & Limitations
• Background: Knowledge Distillation
• Interpretation: More Training?
• Approach: Truncated Softmax

Introduction: Transformer Success & Limitations

Recent transformer models have reached unparalleled success in Natural Language Processing. After GPT, BERT, and GPT-2 are released, they keep pushing the state of the art in question answering, translation, reading comprehension, text summarization, and more! As they become more powerful, they also become larger and larger, causing them to take up more RAM and have longer wait time for inference. To use a transformer back a resource for someone seeking resources online in the United States, it is imperative that this resource be available on mobile as most people have access to the internet on their smartphones but not everyone has a laptop. With the newest development of transformers Natural Langauge Processing GPT-2 reaching 1.5 billion parameters, it is necessary to reduce the size of these transformers to ensure mobile support. I will describe the transformer model to present ways we can reduce it’s size!

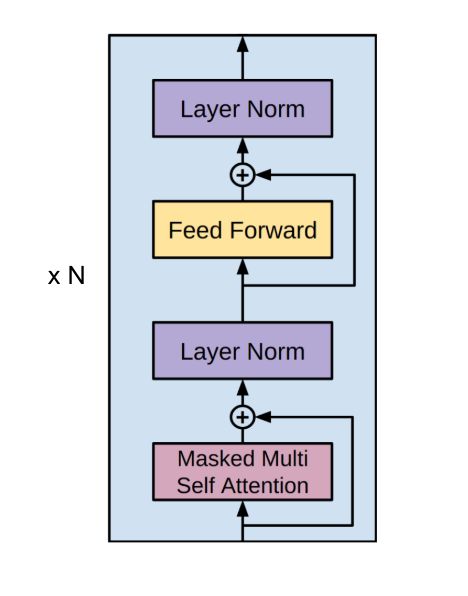
We shall look at the transformer at the highest level and then zoom into its components. The transformer is composed of stacking multiple transformer blocks! Words are first represented as vectors (rank 1 tensor), and thus a sequence of words is represented as a list of tensors (rank 2 tensor). This data flowing through a transformer block encounters a multi-headed attention unit, and residually connects to a Layer Normalization Unit. The output of this layer normalization connects directly to a Feed-Forward Network, and residually connects to the output of the Feed-Forward Network to another Layer Normalization Unit.

Layer normalization takes inputs, and each input is normalized along the feature dimension. The Feed-Forward network takes an input and combines each of it’s features for a new representation. The residual connections help propagate features that could be altered or lost during the The expressive power of the Transformer comes from its use of attention, so we will pay special attention to the mutli-headed attention unit.

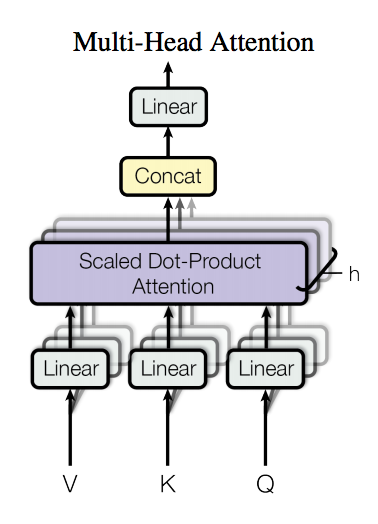
The multi-headed attention unit first takes the vector representation of words, and then projects these vectors to many lower-dimensional sub-spaces. Each of these lower dimensional subspaces can be interpreted as a vector space that emphasizes on certain aspects of human language for a word. So if our multi-headed attention unit has 8 heads, it’s possible that one of these heads projects our word vectors into a space that focuses on the sad aspect of words.

For each of these subspaces, the Transformer computes attention on the projected vectors, and concatenates the output of these attention computations so we are in the same dimensional vector space as we started off in. The attention computation itself gives us the inductive bias that makes transformers so much more successful than Recurrent Neural Networks. This inductive bias is that each word in a sequence pays a certain amount of attention to the other words in the sequence, paying more attention to the other words that are relevant while paying little to no attention to the irrelevant words. This is structured into the scaled dot-product attention. Scaled dot-product attention is computed as such:

The sequences of word vectors (rank 2 tensors) that were projected to lower dimensional subspaces are dotted together, they are scaled by the dimension of the vector, and then the softmax across the sequence is computed. This softmax vector is dotted with projected word vectors. This assigns a weight to each word in the sequence, the amount of attention to pay to that word.

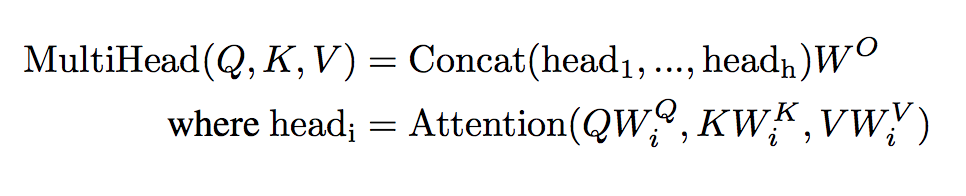
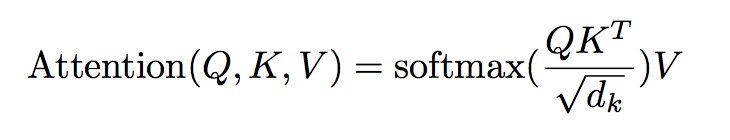
Thus, in order to have smaller transformer model, we have the option of reducing the number of transformer blocks, we can reduce the original dimension of the word vectors, we can reduce the projected word vector dimension, or we can reduce the number of heads in the multi-headed attention unit.

Background: Knowledge Distillation

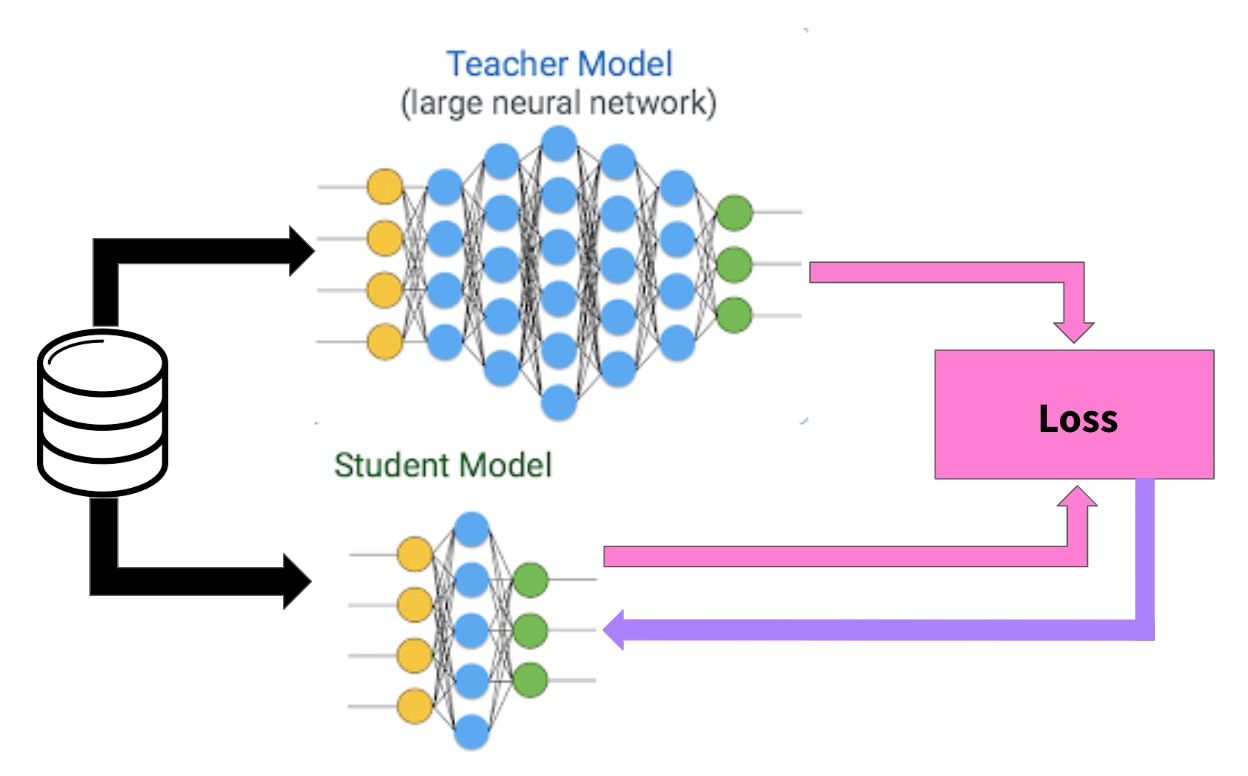
You can think of knowledge distillation as having a larger, well trained teacher neural network that teaches a smaller neural network how to perform like itself. You feed both neural networks the same data, and in the loss function you reward the student for producing an output similar to the teacher, and update the parameters of the student network via backpropagation when it’s output is not similar to the teacher’s. The idea is that if we can get the smaller student network to produce similar outputs as the larger teacher network, it is essentially performing just as well.

To be more specific, in this case when training the transformer as a language model, we start off with a sequence of words and we mask some of those words and tell the transformer to try to predict the right word.

After predicting a word, normally the loss function is the cross-entropy loss. You would dot a one-hot encoded vector $\mathbf{1}\{ y_j=k\}$ with the log output of the neural network $\log p(y_j=k | \mathbf{x};\theta)$, which is a log probability vector assigning each word in the vocabulary a probability.

However, for knowledge distillation you dot the output of the teacher network $q(y_j=k | \mathbf{x};\theta)$ with the log output of the student neural network $\log p(y_j=k | \mathbf{x};\theta)$. This means that you want the student to predict not just the right masked word, and you also want the student network to consider the other words the teacher was considering. We would hope that teacher network has developed a rich understanding of human language, and would thus not just consider the correct word with high probability but also reasonable synonyms, and thus we want to distill this knowledge to the student network.

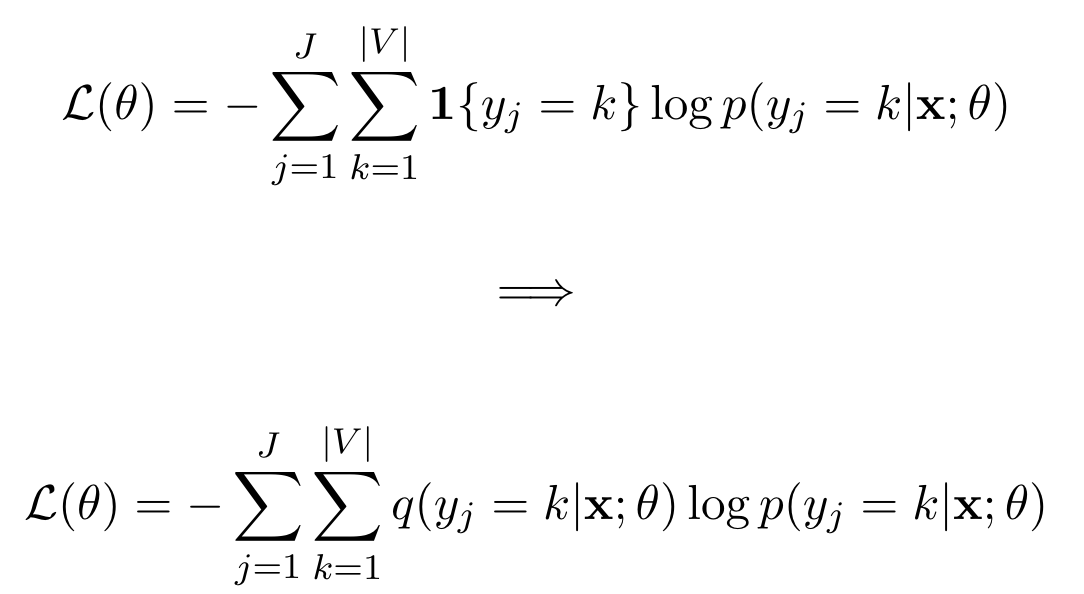
Interpretation: More Training?

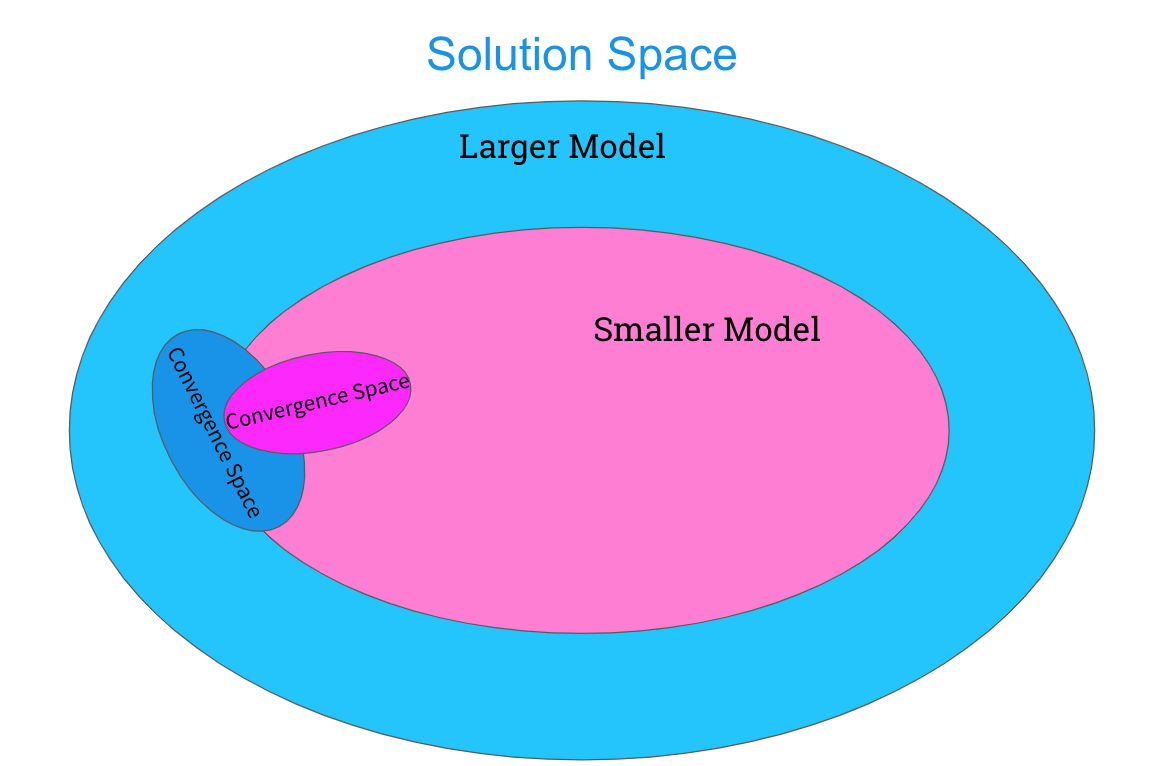
Knowledge distillation also has an intuitive interpretation. When considering a particular model, we can say it has a certain capacity to represent functions in solution space. Bigger models with more parameters are more flexible and have a higher capacity to learn more, and can thus represent more functions in solution space. Thus, transformers with more blocks, higher vector dimensions or higher projection dimensions can represent more functions in solution space and can thus converge to better solutions in this expanded solution space.

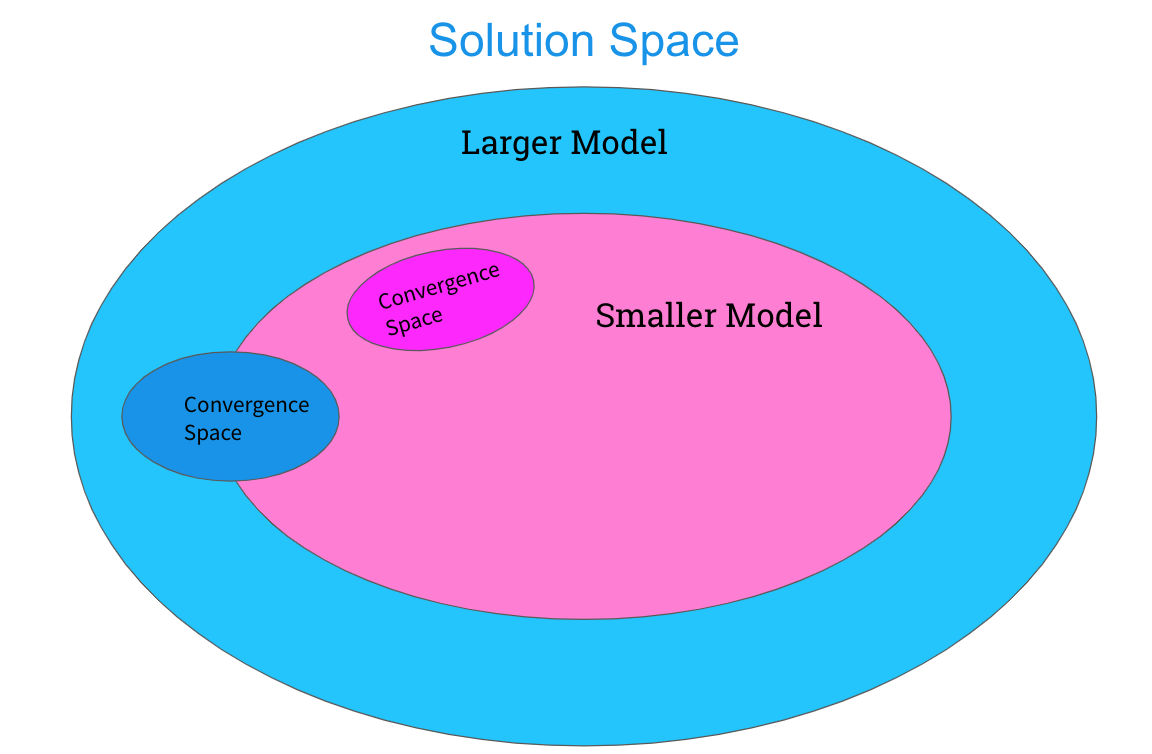
When considering a smaller network, we know that it can represent fewer functions in solution space, and if we train it the same way as a larger network we know it converges to a different solution than the larger network since it’s performance is different. However, we know there is an overlap between the solution space of the larger and smaller networks. If we hope to have successful knowledge distillation, we imagine that there is a region in solution space that the larger neural network tends to converge to that has some overlap with the solution space of the smaller network. Thus, by training the student network with the outputs of the teacher network, we hope to drive the smaller student network to converge to a solution in the region where the teacher could converge.

Approach: Truncated Softmax

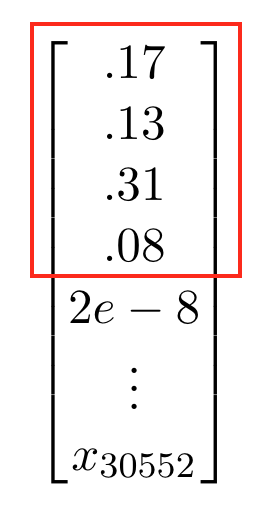
When performing knowledge distillation for a language model, we have to deal with memory constraints as GPU’s, TPU’s, or even CPU’s only have so much RAM. If we save the outputs of the teacher network as data, and load it into RAM, for each word we are loading a vector of the same dimension as your vocabulary. In this case, for each word we had 30,522 dimensional vector.

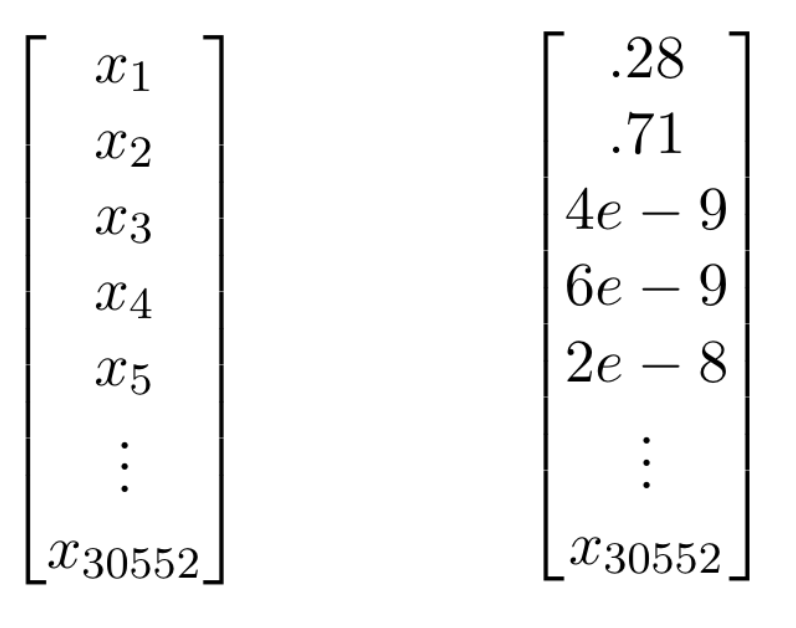
This large vector made it impossible to have adequate batch-sizes and sequence lengths, parameters crucial training a neural network. Moreover, each of these probability vectors was actually really low in information. In a 30,522 word vocabulary, when predicting a masked word most of those words are going to have essentially zero probability. There are only so many reasonable words or synonyms that a well trained teacher network would assign any considerable probability to. Thus it was best to save the top-k probable words and their probabilities from the teacher network instead of the whole probability network.